:`(PERSAMAAN DAN PERTIDAKSAMAAN NILAI MUTLAK)`:

 Persamaan Nilai Mutlak

Persamaan ditandai dengan menggunakan tanda sama dengan (=).

Biasanya, sebuah soal persamaan nilai mutlak akan meminta kita untuk mencari himpunan penyelesaian dari persamaan tersebut menggunakan aljabar dan sifat-sifat yang ada pada nilai mutlak.

Contoh Soal:

1. Carilah himpunan penyelesaian dari |x + 1| = 2x – 3.

Jawab:

 

 

2. Tentukan himpunan penyelesaian dari .

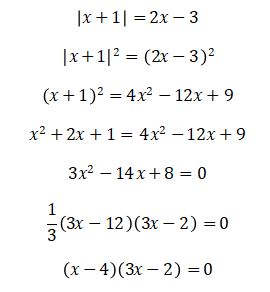
Jawab:

 

3. Berapa hasil x untuk persamaan nilai mutlak |6 – 2x| – 11 = 13

Solusi:

|6 – 2x| – 11 = 13

|6 – 2x| = 24

Setelah itu mari kita mencari nilai x.

6 – 2x = 24

-2x = 24 – 6

-2x = 18

2x = -18

x = -9

dan

6 – 2x = -24

-2x = -24 – 6

-2x = -30

-x = -15

x = 15

 

Pertidaksamaan Nilai Mutlak

Pertidaksamaan adalah kalimat matematika terbuka yang memuat ungkapan >, ≥, <, atau ≤. Sedangkan ketidaksamaan atau pertidaksamaan mutlak (absolut) adalah pertidaksamaan yang selalu benar untuk setiap nilai pengganti variabelnya. Suatu pertidaksamaan yang selalu salah untuk setiap pengganti variabelnya disebut pertidaksamaan palsu.

Sifat-Sifat Pertidaksamaan

Tanda pertidaksamaan tidak berubah jika kedua ruas ditambah atau dikurangi dengan bilangan yang sama.

Jika a < b maka:

a + c < b + c
a – c < b – c

---

Tanda pertidaksamaan tidak berubah jika kedua ruas dikali atau dibagi dengan bilangan positif yang sama.

Jika a < b, dan c adalah bilangan positif, maka:

• a.c < b.c
• a/b < b/c

---

Tanda pertidaksamaan akan berubah jika kedua ruas pertidaksamaan dikali atau dibagi dengan bilangan negatif yang sama

Jika a < b, dan c adalah bilangan negatif, maka:

 

Tanda pertidaksamaan akan berubah jika kedua ruas pertidaksamaan dikali atau dibagi dengan bilangan negatif yang sama

Jika a < b, dan c adalah bilangan negatif, maka:

• a.c > b.c
• a/c > b/c

Tanda pertidaksamaan tidak berubah jika kedua ruas positif masing-masing dikuadratkan

Jika a < b; a dan b sama-sama positif, maka: a2 < b2

Penyelesaian:

1. Ruas kanan dibuat menjadi nol
2. Faktorkan

• Tentukan harga nol, yaitu nilai variabel yang menyebabkan nilai faktor sama dengan nol

Gambar garis bilangannya

1. Jika tanda pertidaksamaan ≥ atau ≤, maka harga nol ditandai dengan titik hitam •
2. Jika tanda pertidaksamaan > atau <, maka harga nol ditandai dengan titik putih °

• Tentukan tanda (+) atau (–) pada masing-masing interval di garis bilangan. Caranya adalah dengan memasukkan salah satu bilangan pada interval tersebut pada persamaan di ruas kiri.
• Tanda pada garis bilangan berselang-seling, kecuali jika ada batas rangkap (harga nol yang muncul 2 kali atau sebanyak bilangan genap untuk pertidaksamaan tingkat tinggi), batas rangkap tidak merubah tanda

---

Tentukan himpunan penyelesaian

→ Jika tanda pertidaksamaan > 0 berarti daerah pada garis bilangan yang diarsir adalah yang bertanda (+)
→ Jika tanda  pertidaksamaan < 0 berarti daerah pada garis bilangan yang diarsir adalah yang bertanda (–)

 

Contoh Soal 

1. Tentukan himpunan selesaian dari pertidaksamaan-pertidaksamaan: ^{|3x + 2|}/₄ ≤ 1 dan |2x – 7| < –5. 

 

 
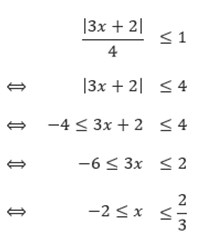
$2.$ Himpunan penyelesaian dari pertidaksaman $|4x-3|\le 1$ adalah . . . .
  Sifat pertidaksamaan harga mutlak adalah:

$|f\left(x\right)|\le a\to -a\le f\left(x\right)\le a$

$|4x-3|\le 1$

sehingga:

$-1\le 4x-3\le 1$

$-1+3\le 4x-3+3\le 1+3$

$2\le 4x\le 4$

$\frac{1}{2}\le x\le 1$

$\mathrm{3.\; Nilai\; x\; yang\; memenuhi\; pertidaksamaan:\; |x2-5x+2|>2\; adalah\; .\; .\; .\; .}$

$\mathrm{Sifat\; pertidaksamaan\; harga\; mutlak\; adalah:\; |f(x)|>a\; \to \; f(x)<-a atau f(x)>a\; |x2-5x+2|>2\; x2-5x+2<-2\; atau\; x2-5x+2>2\; Solusi\; I:\; x2-5x+2<-2\; x2-5x+4<0\; (x-1)(x-4)<0\; 1<x<4\; .\; .\; .\; .\; (*)}$

Daftar Pustaka

Persamaan

https://rumuspintar.com/nilai-mutlak/

https://www.kelaspintar.id/blog/tips-pintar/persamaan-dan-sifat-sifat-nilai-mutlak-beserta-contoh-soalnya-11005/

https://edura.id/blog/matematika/persamaan-nilai-mutlak/  

 

Pertidaksamaan

https://www.dosenpendidikan.co.id/pertidaksamaan-nilai-mutlak/ 

https://www.maretong.com/2019/08/Soal-dan-pembahasan-persamaan-dan-pertidaksamaan-nilai-mutlak.html#toc5 

 https://soalkimia.com/soal-pertidaksamaan-nilai-mutlak/

Gambar*

https://pixabay.com/id/photos/sempoa-kelas-count-konter-1866497/ 

https://pixabay.com/id/illustrations/matematika-papan-tulis-pendidikan-1500720/

*gambar-gambar lainnya didapatkan dari sumber-sumber yang tertera