==== FUNGSI KUADRAT, RASIONAL, DAN IRASIONAL ====
FUNGSI KUADRAT, RASIONAL, DAN IRASIONAL
[][][][][][][][][][][][][][][][][][][][][][][][][][][][][][][][][][][][][][][][][][][][][][][][][][][][][][][][][][][][][][]FUNGSI KUADRAT
Pengertian
Fungsi kuadrat adalah sebuah fungsi polinom yang memiliki peubah/variabel dengan pangkat tertingginya adalah 2 (dua).
Secara umum fungsi kuadrat memiliki bentuk umum seperti berikut ini:
f(x) = ax2 + bx + c, a ≠ 0
dengan f(x) = y yang merupakan variabel terikat, x adalah variabel bebas, sedangkan a, dan b merupakan koefisien dan c adalah suatu konstanta.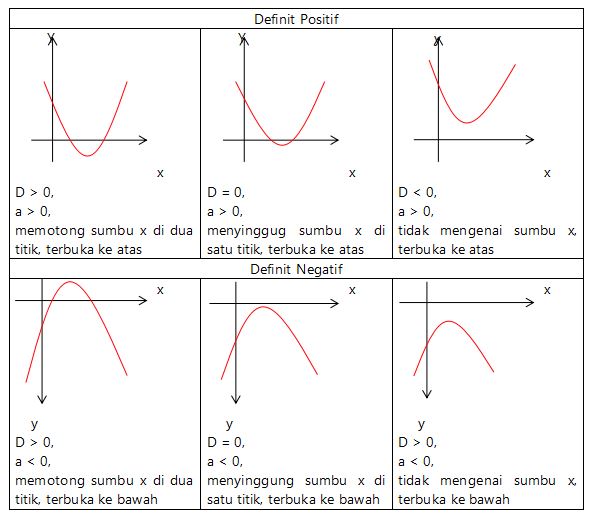
Contoh Fungsi Kuadrat
Contoh Soal Fungsi Kuadrat
Contoh Soal 1
Jika grafik mempunyai titik puncak (1, 2), tentukan nilai a dan b. (UMPTN ’92)
Pembahasan 1:
Gunakan rumus sebagai nilai x titik puncak, sehingga:
Substitusi titik puncak (1, 2) ke dalam persamaan diperoleh:
Dari persamaan baru, substitusikan nilai ,maka:
Contoh Soal 2
Jika fungsi mempunyai sumbu simetri x = 3, tentukan nilai maksimumnya. (UMPTN ‘00)
Pembahasan:
Sumbu simetri berada di x titik puncak, sehingga:
Sehingga fungsi y menjadi:
Nilai maksimumnya:
Soal 3
Tentukan grafik yang melintasi (-1, 3) dan titik minimumnya sama dengan puncak grafik . (UMPTN ‘00)
Pembahasan:
Titik puncak adalah:
Substitusikan nilai dan
dalam persamaan:
Maka grafik fungsi kuadrat yang dicari adalah:
Fungsi Rasional
Pengertian
Fungsi rasional adalah fungsi yang memetakan suatu bilangan real x ke bilangan rasional Fungsi rasional yang paling sederhana adalah fungsi y = 1/x dan fungsi y = 1/x², yang keduanya memiliki pembilang konstanta dan penyebut polinomial dengan satu suku, serta kedua fungsi tersebut memiliki domain semua bilangan real kecuali x ≠ 0.
Fungsi ini disebut juga sebagai fungsi kebalikan karena setiap kita mengambil sembarangx (kecuali nol) maka akan menghasilkan kebalikannya sebagai nilai dari fungsi tersebut. Hal ini berarti x yang besar akan menghasilkan nilai fungsi yang kecil, demikian pula sebaliknya. Tabel dan grafik dari fungsi tersebut dapat dilihat seperti di bawah ini.

Contoh Soal
Sketsa grafik fungsi rasional Sketsa grafik fungsi rasional dapat digambarkan dengan menentukan asimtotnya dan menentukan beberapa titik yang dilaluinya. Asimtot merupakan garis yang tidak dipotong oleh grafik, tetapi hanya didekati sampai tak hingga.
#Langkah 1, Menentukan Asimot Datar
Bentuk umum fungsi rasional adalah memiliki asimtot datar
sehingga
memiliki asimtot datar
.
#Langkah 2, Menentukan Asimot Tegak
Penyebut dari fungsi rasional adalah
.
Pembuat nol penyebut :
Sehingga asimtot tegak dari fungsi rasional adalah
.
#Langkah 3, Menentukan Tititk koordinat bantu
Suatu pertidaksamaan bentuk akar dinamakan juga pertidaksamaan irasional, hal ini dikarekanan nilai peubah yang akan ditentukan selangnya terdapat dalam tanda akar. Teoremanya adalah sebagai berikut:
1.

2.

3.

4.
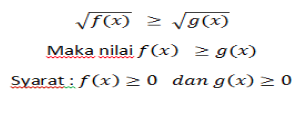



Komentar
Posting Komentar