Sistem Pertidaksamaan Linear 2 Variabel

Pertidaksamaan Linear Dua Variabel Adalah suatu kalimat terbuka dalam ilmu matematika yang di dalamnya terdapat 2 (dua) variabel. Dengan masing – masing dari variabel berderajat satu dan dihubungkan dengan tanda ketidaksamaan.

Tanda ketidaksamaan yang dimaksud disini adalah seperti >, <, ≤, atau ≥. Maka bentuk dari pertidaksamaan linear bisa dituliskan seperti dibawah ini.

• ax + by < c
• ax + by > c
• ax + by ≤ c
• ax + by ≥ c

Dan berikut ini adalah contoh dari pertidaksamaan dalam kalimat matematika nya.

• 4x – y < 9
• 2x + 3y > 6

Beberapa kalimat di atas menggunakan tanda hubung seperti >, <, > atau menggunakan <. Tanda tersebut adalah tanda yang menandakan kalimat tersebut adalah kalimat pertidaksamaan.

Pertidaksamaan Linear Dua Variabel (SPtLDV)

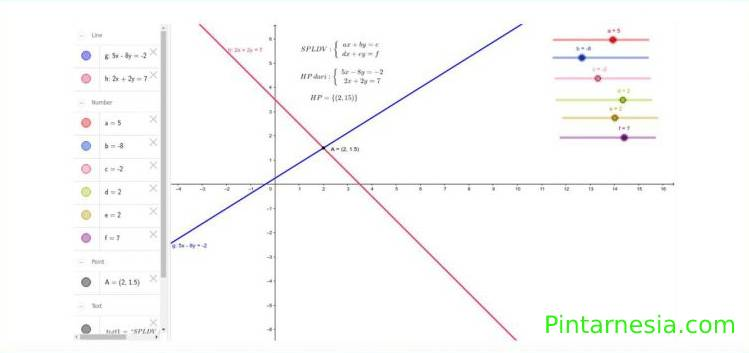
Berbeda dengan penyelesaian dari SPLDV (Sistem Persamaan Linear Dua Variabel) yang berwujud himpunan titik – titik. Atau jika kita gambar grafiknya akan berupa garis lurus. Penyelesaian dari pertidaksamaan linear dua variabel adalah daerah penyelesaian.

Dalam praktiknya penyelesaian pertidaksamaan linear bisa berwujud daerah yang diarsir atau pun daerah penyelesaian pertidaksamaan linear dua variabel berupa daerah yang bersih.

Untuk menentukkan daerah penyelesaiannya, kita bisa melakukan langkah – langkah seperti yang ada di bawah ini.

• Ubah tanda ketidaksamaan dari pertidaksamaan menjadi tanda sama dengan (=), sehingga kita mendapatkan persamaan linear dua variabel.
• Gambar dari grafik atau pun garis dari persamaan linear dua variabel tadi. Hal tersebut bisa kita lakukan dengan cara menentukan titik potong sumbu x dan sumbu y dari persamaan. Atau juga bisa menggunakan 2 (dua) titik sembarang yang dilewati oleh garis. Garis akan membagi 2 (dua) bidang kartesius.
• Lakukan uji titik yang tidak dilewati oleh garis (substitusi nilai x dan substitusi nilai y ke pertidaksamaan). Jika menghasilkan pernyataan yang benar, artinya daerah tersebut adalah penyelesaiannya. Tapi jika menghasilkan  pernyataan salah maka bagian lainnya yang merupakan penyelesaiaannya.